Be brave, go ahead and divide by zero

When you learned division in school, the teacher probably brushed off the issue of dividing by zero in one sentence: you can’t do it, moving on. You might feel like you got shortchanged by that explanation. Why not? What happens when you divide by zero?

You can’t ask the computer. Computers fail when you ask them questions with no unambiguous answer. Dividing by zero is just such a question. Folklore suggests that asking the computer to divide by zero makes it spectacularly explode or something. In reality, it returns an error message or the reply Not A Number, or it gives a wrong answer, or the program terminates, or sometimes the machine falls into an infinite loop.

The internet’s favorite divide-by-zero error is the one that temporarily crippled the USS Yorktown, a Ticonderoga-class cruiser that was the test bed for the Navy’s Smart Ship program. When a crew member typed zero into a database field, the computer tried to divide by it, crashing the system badly enough to cripple the ship’s navigation systems for several hours.

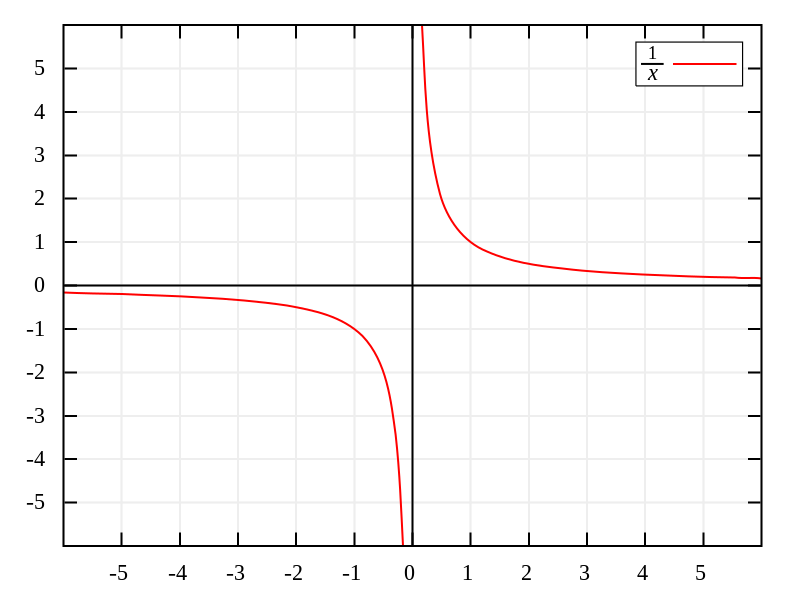
Humans are smarter than computers in some ways, and we’re capable of coming up with creative answers to seemingly unanswerable questions. So what do you get when you divide something by zero? My answer draws heavily on the entertaining wikipedia article. For the sake of simplicity, let’s say we’re dividing one by zero. The math people have a crafty method for dealing with problems you can’t approach directly. You can edge closer and closer to the problem and see if you converge on an answer. So instead of dividing one by zero, you could try dividing it by smaller and smaller numbers that approach zero. One divided by one tenth is ten. One divided by one one-hundredth is a hundred. One divided by one one-thousandth is a thousand. Since one divided by one one-gazillionth is one gazillion, logic suggests that one divided by zero is going to be infinity.

It makes sense, but there’s a problem. We’ve been approaching zero from above, but we could just as easily approach it from below. When you divide one by negative one tenth, you get negative ten. One divided by negative one one-hundredth is negative one hundred. One divided by negative one gazillionth is negative one gazillion. So you could just as easily say that one divided by zero is negative infinity. Both infinity and negative infinity are equally valid answers. Here it is as a graph.

Some people interpret this graph to say that infinity and negative infinity are the same number. It’s not as crazy as it sounds. Let’s say that instead of being on the computer screen, the graph was drawn on a globe. Imagine the number line wrapped around the equator. Say the spot where the Prime Meridian crosses the equator is zero. If you’re in a rowboat bobbing in that spot in the Atlantic Ocean, enjoying the warm breeze, you can think of the positive numbers as going off along the equator to the east, and the negative numbers going off to the west. Infinity is the farthest possible point away from you on the equator to the east, and negative infinity is the farthest point away from you to the west. On the Earth, positive and negative infinity are the same place, the International Date Line in the Pacific. For this image to be totally accurate, the Earth would have to be infinitely large, but the math guys bracket that. By this thinking, one divided by zero does have a single, unambiguous answer: this mysterious number called unsigned infinity.

When you type “divide by zero” into Google images, you get a lot of stuff like this:

Our European-descended philosophical assumptions are at work here. Western thinkers prefer clear, unambiguous, yes-no dichotomies. Paradoxical and multiply-determined truths make us anxious. Some of the internet cartoons show dividing by zero ripping holes in the space-time continuum, forming black holes, or making your head explode. That much hyperbole has to conceal some pretty intense anxiety. I know these pictures are jokes, but I agree with Freud, on some level there are no jokes.