The chromatic circle and the circle of fifths

The heart of Western tonal theory is this diagram:

It’s called the chromatic circle, and it shows all of the notes you can play with a piano keyboard or guitar fretboard. It is closely related to another extremely important diagram called the circle of fifths:

In this post, I explain where these diagrams come from and what they mean.

Imagine a guitar string tuned to play C3, a note with a frequency of 1 Hz. In other words, the guitar string is vibrating to and fro one time per second. (The actual frequency of C3 is 130.8128 Hz, so a string tuned to C3 will vibrate to and fro 130.8128 times per second. Multiply every frequency in this post by 130.8128 for the real values.) When you pluck the string, it doesn’t just bow back and forth along its entire length, it squiggles around in a complex and evolving way. The string’s motion is the combination of many different simple vibrations added together. Each of these component vibrations is called a harmonic, and each harmonic produces its own distinct pitch. This means that every note on the guitar is actually a whole stack of different pitches. By carefully touching a guitar string in different locations, you can isolate the harmonics; they have a mysterious sound, ghostly and pure.

Horn players use harmonics constantly.

The math of harmonics is surprisingly simple. Our hypothetical C string has a fundamental frequency (first harmonic) of 1 Hz, so its other harmonics are at 2 Hz, 3 Hz, 4 Hz, 5 Hz, and so on up to infinity (though as a practical matter you can only hear the lowest harmonics, because they get quieter as you go up.) We will talk about the pitches that these harmonics produce below.

Now imagine another guitar string tuned to play C4, the note an octave higher than C3. The fundamental frequency of C4 is 2 Hz. If its frequency is twice that of C3, then why is it also called C? How can it have the same name if it is not at all the same note? We can find the answer by looking at C4’s harmonics. Its harmonics are at 2 Hz, 4 Hz, 6 Hz, 8 Hz, 10 Hz, and all the multiples of two up to infinity. The original C3 string has all of those same harmonics.  

The shared harmonic relationship between C3 and C4 is enough to convince Western people that these two notes are functionally equivalent. The same is true of any two notes whose fundamental frequencies are related by powers of two. If the note with a fundamental frequency of 1 Hz is called C, then so are the notes whose fundamental frequencies are 2 Hz, 4 Hz, 8 Hz and 16 Hz, and so are the notes whose fundamental frequencies are 1/2 Hz, 1/4 Hz, 1/8 Hz and 1/16 Hz. These notes will all behave the same way in chords, and for Western music theory purposes, that is enough to think of them as being “the same.” In the rest of the post, I will be freely multiplying and dividing the notes’ frequencies by two in order to keep them all as close together as possible.

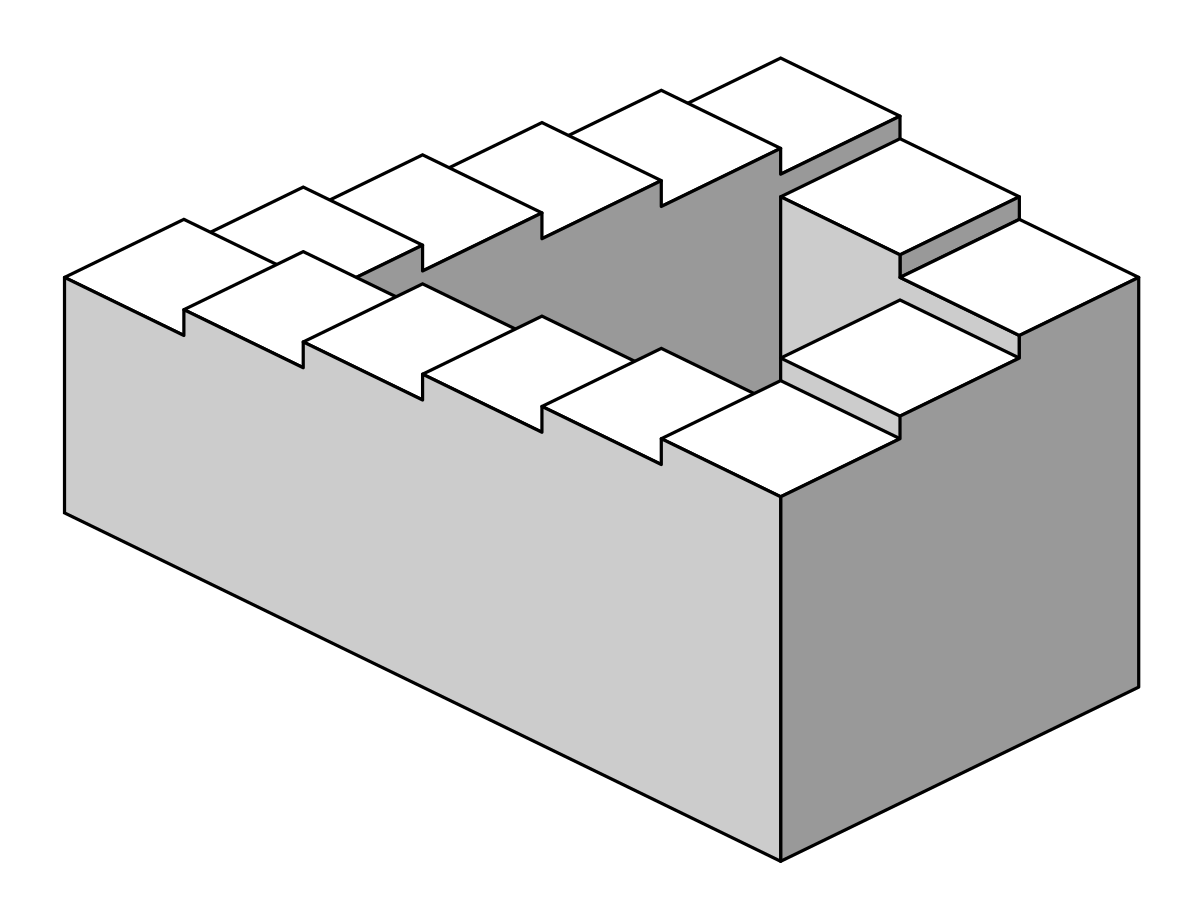
The upshot here is that octave equivalence gives pitch space the topology of Penrose stairs – you keep going up or down, but you keep retreading the same space.

In real life, pitch space is a spiral, because the C at 2 Hz is in fact higher than the C at 1 Hz, and it’s lower than the C at 4 Hz. But pitch class space is a Penrose staircase.

To understand Western harmony, you also need to know about the third harmonic. Its frequency is three times that of the fundamental. The third harmonic of C3 at 1 Hz is G4 at 3 Hz. If you bring that G down an octave, you get G3 at 3/2 Hz, which is a perfect fifth above C3. Two notes that are a perfect fifth apart don’t have as much overlap in their harmonic series as an octave does, but they still overlap quite a bit.

To go up a perfect fifth from any note, you multiply its fundamental frequency by 3/2, and to go down a perfect fifth from any note, you divide its fundamental frequency by 3/2. Medieval Europeans built a tuning system entirely out of perfect fifths called Pythagorean tuning. This system is also called three-limit just intonation, because it is based on the first three harmonics.

This diagram sort of resembles the circle of fifths, but it isn’t a circle, it’s a spiral. In Pythagorean tuning, F-sharp and G-flat are two different notes. So are C-sharp and D-flat, and G-sharp and A-flat. Each pair is pretty close to having the same frequency, but not close enough. Wouldn’t it be nice if we could tie this spiral into a circle? 

Western Europe tried lots of other tuning systems before eventually settling on twelve-tone equal temperament (12-TET). In this system, you define all the intervals in terms of semitones. To go up a semitone from any note, you multiply its frequency by the twelfth root of two. To go down a semitone from any note, you divide its frequency by the twelfth root of two. Rather than having F-sharp and G-flat be different notes, you just split the difference and tune them the same.

In 12-TET, a fifth is seven semitones, so to go up a fifth from C, you multiply its frequency by two to the seven twelfths power. This turns out to be a very good approximation of multiplying its frequency by 3/2.

In 12-TET, the major thirds are sharper than you would ideally like, and the minor thirds are flatter than you would ideally like. The best-sounding thirds come from the fifth harmonic, but if you try to tune using the first five harmonics, pitch space becomes a complex network that is full of conflicts. In 12-TET, you have to live with slightly out-of-tune thirds, but pitch space gets a heck of a lot simpler.

One nice thing about 12-TET is the intriguing relationship between the chromatic circle and the circle of fifths. You can transform one into the other by flipping every alternate note with the one that’s a tritone away.

Notice that one of the whole tone scales is the same across both circles, while the other one gets mirror-imaged.

Can you turn the chromatic circle and the circle of fifths into music? I tried.

Here’s a chart. The dotted line shows the awkward transition from sharps to flats.

Here’s a possible harmonization.

Figuring out the accidentals for this was horrible, but more to the point, it doesn’t sound very good. This is not because of my lack of melody-writing ability. I don’t think there is a good-sounding way to systematically permute all of pitch class space. 12-TET fifths are very close to three-limit just intonation fifths, and you don’t really notice the difference in most real-world music. But when you work all the way through the circle of fifths, something just doesn’t intuitively add up. You see it most clearly in notation when you have to do that brute-force jump from the flats to the sharps, or vice versa. This is not just an issue of semantics or terminology; it illustrates the “empty calories” feeling to the whole exercise. Each individual V-I resolution makes sense, but taken as a whole, the circle feels like a conspiracy theory, a series of seemingly logical but actually tautological arguments.

Would it be more satisfying to systematically work through pitch-class space out of order? Maybe? That’s the point of twelve-tone serialism.

I have never heard a tone row that I needed to hear twice, but I’m a philistine when it comes to high modernism. I do love those Thelonious Monk tunes that freefall through the circle of fifths via alternating whole-tone scales, but he never goes all the way around, and he’s always gesturing at an underlying folkloric basis for his abstractions, e.g. rhythm changes.

Anyway, maybe the full circle is not useful for actual musical expression, but it still has pedagogical and conceptual value. I do enjoy exploring the beautiful Notenscheibe by Paul Bretschneider. Writing scales on the circle of fifths is enlightening: the major scale and all of its modes are all contiguous, and you can move through them in musically logical ways to each other by rotating them around the circle. The whole tone scale and the diminished scale look the same on the circle of fifths as they do on the chromatic circle.

It’s easy to get carried away with all the combinatorics. Remember that all of this is just an approximation of the actually good-sounding intervals that you get from harmonics. Also, it’s important not to lose sight of musical time, which is the thing that gives all of this meaning to begin with. Harmony is fun, but it only makes sense in the context of rhythm.